7538. Переворот карт

Майк и его юная дочь Джесси играют в новую карточную игру, предназначенную для детей. Правила довольно просты, каждый игрок получает набор карт. Каждая карта имеет одну картинку на каждой стороне. Они ходят по очереди, и первый кто избавится от игральных карт, является победителем.

Ход игрока состоит в выборе некоторого подмножества имеющегося у него карт и выкладки их на стол. Но имеется одно правило: карты должны быть размещены на столе так, чтобы никакие две из них не показывали одну и ту же картинку.

Майк подумал, что было бы очень уместно сыграть со своим ребенком из-за простых правил. Майк также полюбил эту игру, потому что нахождение наилучшей стратегии является алгоритмически интересной задачей!

Помогите Майку определить, сможет ли он выложить все карты на стол за один ход.

Вход. Первая строка содержит количество тестов t (t ≤ 10). Каждый тест начинается количеством карт n (1 ≤ n ≤ 50 000) на руках у Майка. Следующие n строк описывают сами карты имеющиеся у Майка.

Картинки на картах представлены числами. i-ая карта задается двумя числами p_i, q_i где 1 ≤ p_i, q_i ≤ 2n.

Выход. Для каждого теста вывести в отдельной строке слово possible если Майк сможет выложить на стол все карты за один ход, и impossible если не сможет.

Пример входа	Пример выхода
3 3 1 2 1 3 2 3 3 1 2 1 2 1 2 1 1 1	possible impossible possible

РЕШЕНИЕ

графы – циклы, система непересекающихся множеств

Анализ алгоритма

Каждой картинке, изображенной на картах, поставим в соответствие одну вершину графа. Каждой карте поставим в соответствие неориентированное ребро (которое соединяет вершины, соответствующие картинкам на сторонах карты). Полученный граф может быть несвязным.

Ответ на задачу будет possible, если каждая компонента связности графа содержит не более одного цикла. Компоненты связности и подсчет циклов в них осуществим при помощи системы непересекающихся множеств.

Пример

Рассмотрим четыре карты. Желтым обозначим стороны карт, которыми они будут расположены вверх. Ребро графа пометим картинкой, которой соответствующая карта будет лежать вверх.

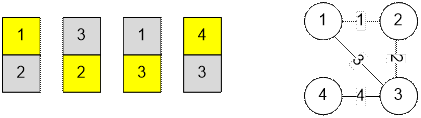
Рассмотрим случай с двумя компонентами связности:

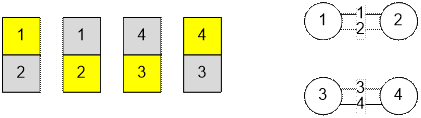
Реализация алгоритма

Определим массивы для обработки данных. Массив dsu используется для системы непересекающихся множеств. Если i – представитель множества, то has_cycle[i] содержит информацию о количестве циклов в нем:

· has_cycle[i] = 0, циклов нет;

· has_cycle[i] = 1, один цикл;

· has_cycle[i] > 1, имеется более одного цикла;

#define MAX 50010

int dsu[2*MAX], has_cycle[2*MAX];

Функция Repr возвращает представителя множества, в котором содержится вершина n.

int Repr(int n)

{

if (n == dsu[n]) return n;

return dsu[n] = Repr(dsu[n]);

}

Объединение множеств, содержащих вершины x и y.

void Union(int x, int y)

{

int x1 = Repr(x), y1 = Repr(y);

Если x и y уже принадлежат одной компоненте связности (они имеют одинакового представителя), и при этом имеется ребро (x, y), то образуется еще один цикл. Добавляем 1 к числу циклов их представителя (x₁ является представителем x и y).

if (x1 == y1)

has_cycle[x1]++;

Если x и y принадлежат разным компонентам связности, при этом y₁ становится представителем множества, то количество циклов для x₁ добавим к числу циклов для y₁.

else

{

dsu[x1] = y1;

has_cycle[y1] += has_cycle[x1];

}

}

Основная часть программы. Читаем входные данные.

scanf("%d",&tests);

while (tests--)

{

scanf("%d",&n);

Инициализируем систему непересекающихся множеств.

for(i = 1; i <= 2*n; i++)

{

dsu[i] = i;

has_cycle[i] = 0;

}

Строим систему непересекающихся множеств.

for (i = 0; i < n; i++)

{

scanf("%d %d",&p,&q);

Union(p,q);

}

Проверяем, содержит ли хоть одна компонента связности более одного цикла.

for (i = 1; i <= 2*n; i++)

if (has_cycle[i] > 1) break;

Выводим ответ.

printf("%s\n",((i <= 2 * n) ? "impossible" : "possible"));

}

Java реализация

import java.util.*;

//import java.io.*;

public class Main

{

static int dsu[], has_cycle[];

static int Repr(int n)

{

if (n == dsu[n]) return n;

return dsu[n] = Repr(dsu[n]);

}

static void Union(int x, int y)

{

int x1 = Repr(x), y1 = Repr(y);

if (x1 == y1)

has_cycle[x1]++;

else

{

dsu[x1] = y1;

has_cycle[y1] += has_cycle[x1];

}

}

public static void main(String[] args) //throws IOException

{

Scanner con = new Scanner(System.in);

//Scanner con = new Scanner(new FileReader ("7538.in"));

int tests = con.nextInt();

while(tests-- > 0)

{

int i, n = con.nextInt();

dsu = new int[2*n+2];

has_cycle = new int[2*n+2];

for(i = 1; i <= 2*n; i++)

{

dsu[i] = i;

has_cycle[i] = 0;

}

for (i = 0; i < n; i++)

{

int p = con.nextInt();

int q = con.nextInt();

Union(p,q);

}

for (i = 1; i <= 2*n; i++)

if (has_cycle[i] > 1) break;

if (i <= 2 * n)

System.out.println("impossible");

else

System.out.println("possible");

}

con.close();

}

}